11-05-2021

The Complexity Of Nonuniform Random Number Generation Pdf To Word

  1. The Complexity Of Nonuniform Random Number Generation Pdf To Word Free
  2. The Complexity Of Nonuniform Random Number Generation Pdf To Word Document
  3. The Complexity Of Nonuniform Random Number Generation Pdf To Word Online
  4. The Complexity Of Nonuniform Random Number Generation Pdf To Word Search
The Complexity Of Nonuniform Random Number Generation Pdf To WordPdf

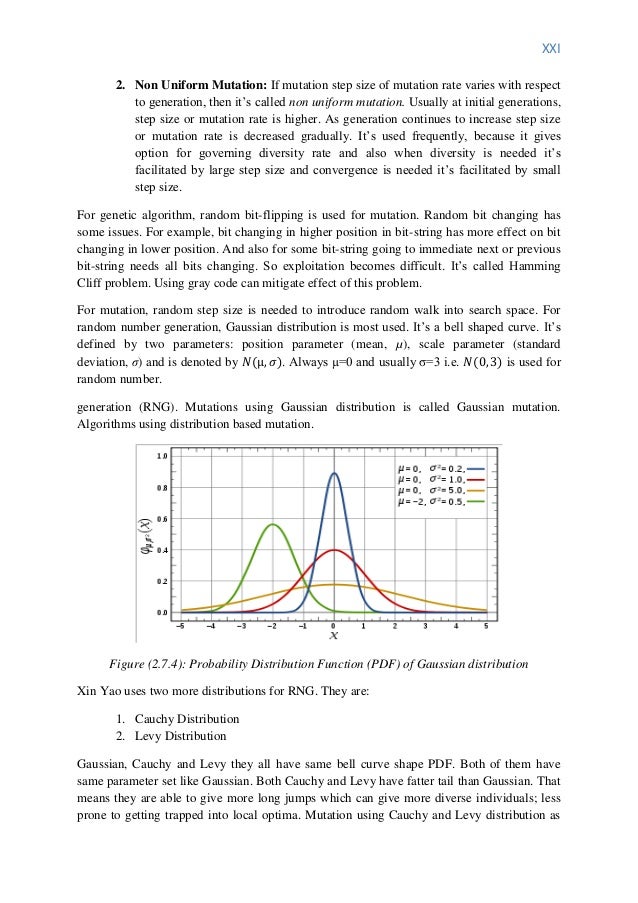
The Complexity Of Nonuniform Random Number Generation Pdf To Word Free

The Complexity Of Nonuniform Random Number Generation Pdf. Of Nonuniform Random Number Generation. Research on uniform random number generation has. Abstract Nonuniform random numbers are key for many technical applications, and designing efficient hardware implementations of non-uniform random number generators is a very active research field. Automatic Nonuniform Random Variate Generation in R Gun¨ ter Tirler and Josef Leydold. Of each probability density function. The designing goals for these methods are fast. Random Number Generation and Monte Carlo Methods. Statistics and Computing. Springer, New York, 1998. Generating non-uniform random numbers. Ask Question 6. Can you tell me any ways to generate non-uniform random numbers? I am using Java but the code examples can be in whatever you want. Random number generator only generating one random number.

The Complexity Of Nonuniform Random Number Generation Pdf To Word Document

Generation

The Complexity Of Nonuniform Random Number Generation Pdf To Word Online

  1. AHRENS, J.H. and DIETER, U. (1974): Computer methods for sampling from gamma, beta, Poisson and binomial distributions. Computing, vol. 12, pp. 223–246.MathSciNetzbMATHCrossRefGoogle Scholar
  2. AKHIEZER, N.I. (1965): The Classical Moment Problem, Hafner, New York.zbMATHGoogle Scholar
  3. ALSMEYER, G. and IKSANOV, A. (2009): A log-type moment result for perpetuities and its application to martingales in supercritical branching random walks.’ Electronic Journal of Probability, vol. 14, pp. 289–313.MathSciNetzbMATHGoogle Scholar
  4. ASMUSSEN, S., GLYNN, P. and THORISSON, H. (1992): Stationary detection in the initial transient problem. ACM Transactions on Modeling and Computer Simulation, vol. 2, pp. 130–157.zbMATHCrossRefGoogle Scholar
  5. BAILEY, R.W. (1994): Polar generation of random variates with the t distribution (1994): Mathematics of Computation, vol. 62, pp. 779–781.MathSciNetzbMATHGoogle Scholar
  6. BONDESSON, L. (1982): On simulation from infinitely divisible distributions. Advances in Applied Probability, vol. 14, pp. 855–869.MathSciNetzbMATHCrossRefGoogle Scholar
  7. BOX, G.E.P. and MÜLLER, M.E. (1958): A note on the generation of random normal deviates. Annals of Mathematical Statistics, vol. 29, pp. 610–611.zbMATHCrossRefGoogle Scholar
  8. CHAMBERS J.M., MALLOWS, C.L. and STUCK, B.W. (1976): A method for simulating stable random variables. Journal of the American Statistical Association, vol. 71, pp. 340–344.MathSciNetzbMATHCrossRefGoogle Scholar
  9. DEVROYE, L. (1981a): The series method in random variate generation and its application to the Kolmogorov-Smirnov distribution. American Journal of Mathematical and Management Sciences, vol. 1, pp. 359–379.MathSciNetzbMATHGoogle Scholar
  10. DEVROYE, L. (1981b): The computer generation of random variables with a given characteristic function. Computers and Mathematics with Applications, vol. 7, pp. 547–552.MathSciNetzbMATHCrossRefGoogle Scholar
  11. DEVROYE, L. (1986a): Non-Uniform Random Variate Generation, Springer-Verlag, New York.zbMATHGoogle Scholar
  12. DEVROYE, L. (1986b): An automatic method for generating random variables with a given characteristic function. SIAM Journal of Applied Mathematics, vol. 46, pp. 698–719.MathSciNetzbMATHCrossRefGoogle Scholar
  13. DEVROYE, L. (1989): On random variate generation when only moments or Fourier coefficients are known. Mathematics and Computers in Simulation, vol. 31, pp. 71–89.MathSciNetzbMATHCrossRefGoogle Scholar
  14. DEVROYE, L. (1991): Algorithms for generating discrete random variables with a given generating function or a given moment sequence. SIAM Journal on Scientific and Statistical Computing, vol. 12, pp. 107–126.MathSciNetzbMATHCrossRefGoogle Scholar
  15. DEVROYE, L. (1996): Random variate generation in one line of code. In: 1996 Winter Simulation Conference Proceedings, Charnes, J.M., Morrice, D.J., Brunner D.T. and Swain J.J. (eds.), pp. 265–272, ACM, San Diego, CA.Google Scholar
  16. DEVROYE, L. (1997): Simulating theta random variates. Statistics and Probability Letters, vol. 31, pp. 2785–2791.MathSciNetCrossRefGoogle Scholar
  17. DEVROYE, L., FILL, J., and NEININGER, R. (2000): Perfect simulation from the quicksort limit distribution. Electronic Communications in Probability, vol. 5, pp. 95–99.MathSciNetzbMATHGoogle Scholar
  18. DEVROYE, L. (2001): Simulating perpetuities. Methodologies and Computing in Applied Probability, vol. 3, pp. 97–115.MathSciNetzbMATHCrossRefGoogle Scholar
  19. DEVROYE, L. and NEININGER, R. (2002): Density approximation and exact simulation of random variables that are solutions of fixed-point equations. Advances of Applied Probability, vol. 34, pp. 441–468.MathSciNetzbMATHCrossRefGoogle Scholar
  20. DEVROYE, L. (2009): On exact simulation algorithms for some distributions related to Jacobi theta functions. Statistics and Probability Letters, vol. 21, pp. 2251–2259.MathSciNetCrossRefGoogle Scholar
  21. DEVROYE, L. and FAWZI, O. (2010): Simulating the Dickman distribution. Statistics and Probability Letters, vol. 80, pp. 242–247.MathSciNetzbMATHCrossRefGoogle Scholar
  22. FILL, J. (1998): An interruptible algorithm for perfect sampling via Markov chains. The Annals of Applied Probability, vol. 8, pp. 131–162.MathSciNetzbMATHCrossRefGoogle Scholar
  23. FILL, J.A. and HUBER, M (2009): Perfect simulation of perpetuities, To appear.Google Scholar
  24. FLAJOLET, P. and SAHEB, N. (1986): The complexity of generating an exponentially distributed variate. Journal of Algorithms, vol. 7, pp. 463–488.MathSciNetzbMATHCrossRefGoogle Scholar
  25. GOLDIE, C.M. and MALLER, R.A. (2000): Stability of perpetuities. Annals of Probability, vol. 28, pp. 1195–1218.MathSciNetzbMATHCrossRefGoogle Scholar
  26. GREEN, P.J. and MURDOCH, D.J. (2000): Exact sampling for Bayesian inference: towards general purpose algorithms (with discussion). In: Monte Carlo Methods, Bernardo, J.M., Berger, J.O., Dawid, A.P. and Smith, A.F.M. (eds.), pp. 301–321, Bayesian Statistics, vol. 6, Oxford university Press, Oxford.Google Scholar
  27. HASTINGS, C. (1955): Approximations for Digital Computers, Princeton University Press, Princeton, New Jersey.zbMATHGoogle Scholar
  28. HÖRMANN, W., LEYDOLD, J., and DERFLINGER, G. (2004): Automatic Nonuniform Random Variate Generation, Springer-Verlag, Berlin.zbMATHGoogle Scholar
  29. HUFFMAN, D. (1952): A method for the construction of minimum-redundancy codes. Proceedings of the IRE, vol. 40, pp. 1098–1101.CrossRefGoogle Scholar
  30. KANTER, M. (1975): Stable densities under change of scale and total variation inequalities. Annals of Probability, vol. 3, pp. 697–707.MathSciNetzbMATHCrossRefGoogle Scholar
  31. KEANE, M.S., and O’BRIEN, G.L. (1994): A Bernoulli factory. ACM Transactions on Modeling and Computer Simulation, vol. 4, pp. 213–219.zbMATHCrossRefGoogle Scholar
  32. KENDALL, W. (2004): Random walk CFTP. Thönnes ed., Department of Statistics, University of Warwick.Google Scholar
  33. KNUTH, D.E. and YAO, A.C. (1976): The complexity of nonuniform random number generation. in: Algorithms and Complexity, Traub, J.E. (ed.), pp. 357–428, Academic Press, New York, N.Y..Google Scholar
  34. MARSAGLIA, G. (1968): Random numbers fall mainly in the planes. Proceedings of the National Academy of Sciences, vol. 60, pp. 25–28.MathSciNetCrossRefGoogle Scholar
  35. MARSAGLIA, G. and ZAMAN, A. (1991): A new class of random number generators. Annals of Applied Probability, vol. 1, pp. 462–480.MathSciNetzbMATHCrossRefGoogle Scholar
  36. METROPOLIS, N., ROSENBLUTH, A., ROSENBLUTH, M., TELLER, A., and TELLER, E. (1953): Equations of state calculations by fast computing machines. Journal of Chemical Physics, vol. 21, p. 1087–1091.CrossRefGoogle Scholar
  37. MURDOCH, D.J. and GREEN, P.J. (1998): Exact sampling from a continous space. Scandinavian Journal of Statistics, vol. 25, pp. 483–502.MathSciNetzbMATHCrossRefGoogle Scholar
  38. PROPP, G.J. and WILSON, D.B. (1996): Exact sampling with coupled Markov chains and applications to statistical mechanics. Random Structures and Algorithms, vol. 9, pp. 223–252.MathSciNetzbMATH3.0.CO%3B2-O'>CrossRefGoogle Scholar
  39. RÖSLER, U. and RÜSHENDORF, L. (2001): The contraction method for recursive algorithms. Algorithmica, vol. 29, pp. 3–33.MathSciNetzbMATHCrossRefGoogle Scholar
  40. K. SATO (2000): Lévy Processes and Infinitely Divisible Distributions, Cambridge University Press, Cambridge.Google Scholar
  41. ULRICH, U. (1984): Computer generation of distributions on the m-sphere. Applied Statistics, vol. 33, pp. 158–163.MathSciNetzbMATHCrossRefGoogle Scholar
  42. VERVAAT, W. (1979): On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Advances in Applied Probability, vol. 11, pp. 750–783.MathSciNetzbMATHCrossRefGoogle Scholar
  43. VON NEUMANN, J. (1963): Various techniques used in connection with random digits. Collected Works, vol. 5, pp. 768–770, Pergamon Press. Also in (1951): Monte Carlo Method. National Bureau of Standards Series, Vol. 12, pp. 36-38.Google Scholar
  44. WILSON, D.B. (2000): Layered multishift coupling for use in perfect sampling algorithms (with a primer on CFTP). In: Monte Carlo Methods, Madras, N. (ed.), pp. 141–176, Fields Institute Communications, vol. 6, American Mathematical Society.Google Scholar
  45. ZOLOTAREV, V. M. (1959): On analytic properties of stable distribution laws. Selected Translations in Mathematical Statistics and Probability, vol. 1, pp. 207–211.Google Scholar
  46. ZOLOTAREV, V. M. (1966): On the representation of stable laws by integrals. Selected Translations in Mathematical Statistics and Probability, vol. 6, pp. 84–88.Google Scholar
  47. ZOLOTAREV, V. M. (1981): Integral transformations of distributions and estimates of parameters of multidimensional spherically symmetric stable laws. In: Contributions to Probability, pp. 283–305, Academic Press.Google Scholar
  48. ZOLOTAREV, V. M. (1986): One-Dimensional Stable Distributions, American Mathematical Society, Providence, R.I..Google Scholar
  1. AHRENS, J.H. and DIETER, U. (1974): Computer methods for sampling from gamma, beta, Poisson and binomial distributions. Computing, vol. 12, pp. 223–246.MathSciNetzbMATHCrossRefGoogle Scholar
  2. AKHIEZER, N.I. (1965): The Classical Moment Problem, Hafner, New York.zbMATHGoogle Scholar
  3. ALSMEYER, G. and IKSANOV, A. (2009): A log-type moment result for perpetuities and its application to martingales in supercritical branching random walks.’ Electronic Journal of Probability, vol. 14, pp. 289–313.MathSciNetzbMATHGoogle Scholar
  4. ASMUSSEN, S., GLYNN, P. and THORISSON, H. (1992): Stationary detection in the initial transient problem. ACM Transactions on Modeling and Computer Simulation, vol. 2, pp. 130–157.zbMATHCrossRefGoogle Scholar
  5. BAILEY, R.W. (1994): Polar generation of random variates with the t distribution (1994): Mathematics of Computation, vol. 62, pp. 779–781.MathSciNetzbMATHGoogle Scholar
  6. BONDESSON, L. (1982): On simulation from infinitely divisible distributions. Advances in Applied Probability, vol. 14, pp. 855–869.MathSciNetzbMATHCrossRefGoogle Scholar
  7. BOX, G.E.P. and MÜLLER, M.E. (1958): A note on the generation of random normal deviates. Annals of Mathematical Statistics, vol. 29, pp. 610–611.zbMATHCrossRefGoogle Scholar
  8. CHAMBERS J.M., MALLOWS, C.L. and STUCK, B.W. (1976): A method for simulating stable random variables. Journal of the American Statistical Association, vol. 71, pp. 340–344.MathSciNetzbMATHCrossRefGoogle Scholar
  9. DEVROYE, L. (1981a): The series method in random variate generation and its application to the Kolmogorov-Smirnov distribution. American Journal of Mathematical and Management Sciences, vol. 1, pp. 359–379.MathSciNetzbMATHGoogle Scholar
  10. DEVROYE, L. (1981b): The computer generation of random variables with a given characteristic function. Computers and Mathematics with Applications, vol. 7, pp. 547–552.MathSciNetzbMATHCrossRefGoogle Scholar
  11. DEVROYE, L. (1986a): Non-Uniform Random Variate Generation, Springer-Verlag, New York.zbMATHGoogle Scholar
  12. DEVROYE, L. (1986b): An automatic method for generating random variables with a given characteristic function. SIAM Journal of Applied Mathematics, vol. 46, pp. 698–719.MathSciNetzbMATHCrossRefGoogle Scholar
  13. DEVROYE, L. (1989): On random variate generation when only moments or Fourier coefficients are known. Mathematics and Computers in Simulation, vol. 31, pp. 71–89.MathSciNetzbMATHCrossRefGoogle Scholar
  14. DEVROYE, L. (1991): Algorithms for generating discrete random variables with a given generating function or a given moment sequence. SIAM Journal on Scientific and Statistical Computing, vol. 12, pp. 107–126.MathSciNetzbMATHCrossRefGoogle Scholar
  15. DEVROYE, L. (1996): Random variate generation in one line of code. In: 1996 Winter Simulation Conference Proceedings, Charnes, J.M., Morrice, D.J., Brunner D.T. and Swain J.J. (eds.), pp. 265–272, ACM, San Diego, CA.Google Scholar
  16. DEVROYE, L. (1997): Simulating theta random variates. Statistics and Probability Letters, vol. 31, pp. 2785–2791.MathSciNetCrossRefGoogle Scholar
  17. DEVROYE, L., FILL, J., and NEININGER, R. (2000): Perfect simulation from the quicksort limit distribution. Electronic Communications in Probability, vol. 5, pp. 95–99.MathSciNetzbMATHGoogle Scholar
  18. DEVROYE, L. (2001): Simulating perpetuities. Methodologies and Computing in Applied Probability, vol. 3, pp. 97–115.MathSciNetzbMATHCrossRefGoogle Scholar
  19. DEVROYE, L. and NEININGER, R. (2002): Density approximation and exact simulation of random variables that are solutions of fixed-point equations. Advances of Applied Probability, vol. 34, pp. 441–468.MathSciNetzbMATHCrossRefGoogle Scholar
  20. DEVROYE, L. (2009): On exact simulation algorithms for some distributions related to Jacobi theta functions. Statistics and Probability Letters, vol. 21, pp. 2251–2259.MathSciNetCrossRefGoogle Scholar
  21. DEVROYE, L. and FAWZI, O. (2010): Simulating the Dickman distribution. Statistics and Probability Letters, vol. 80, pp. 242–247.MathSciNetzbMATHCrossRefGoogle Scholar
  22. FILL, J. (1998): An interruptible algorithm for perfect sampling via Markov chains. The Annals of Applied Probability, vol. 8, pp. 131–162.MathSciNetzbMATHCrossRefGoogle Scholar
  23. FILL, J.A. and HUBER, M (2009): Perfect simulation of perpetuities, To appear.Google Scholar
  24. FLAJOLET, P. and SAHEB, N. (1986): The complexity of generating an exponentially distributed variate. Journal of Algorithms, vol. 7, pp. 463–488.MathSciNetzbMATHCrossRefGoogle Scholar
  25. GOLDIE, C.M. and MALLER, R.A. (2000): Stability of perpetuities. Annals of Probability, vol. 28, pp. 1195–1218.MathSciNetzbMATHCrossRefGoogle Scholar
  26. GREEN, P.J. and MURDOCH, D.J. (2000): Exact sampling for Bayesian inference: towards general purpose algorithms (with discussion). In: Monte Carlo Methods, Bernardo, J.M., Berger, J.O., Dawid, A.P. and Smith, A.F.M. (eds.), pp. 301–321, Bayesian Statistics, vol. 6, Oxford university Press, Oxford.Google Scholar
  27. HASTINGS, C. (1955): Approximations for Digital Computers, Princeton University Press, Princeton, New Jersey.zbMATHGoogle Scholar
  28. HÖRMANN, W., LEYDOLD, J., and DERFLINGER, G. (2004): Automatic Nonuniform Random Variate Generation, Springer-Verlag, Berlin.zbMATHGoogle Scholar
  29. HUFFMAN, D. (1952): A method for the construction of minimum-redundancy codes. Proceedings of the IRE, vol. 40, pp. 1098–1101.CrossRefGoogle Scholar
  30. KANTER, M. (1975): Stable densities under change of scale and total variation inequalities. Annals of Probability, vol. 3, pp. 697–707.MathSciNetzbMATHCrossRefGoogle Scholar
  31. KEANE, M.S., and O’BRIEN, G.L. (1994): A Bernoulli factory. ACM Transactions on Modeling and Computer Simulation, vol. 4, pp. 213–219.zbMATHCrossRefGoogle Scholar
  32. KENDALL, W. (2004): Random walk CFTP. Thönnes ed., Department of Statistics, University of Warwick.Google Scholar
  33. KNUTH, D.E. and YAO, A.C. (1976): The complexity of nonuniform random number generation. in: Algorithms and Complexity, Traub, J.E. (ed.), pp. 357–428, Academic Press, New York, N.Y..Google Scholar
  34. MARSAGLIA, G. (1968): Random numbers fall mainly in the planes. Proceedings of the National Academy of Sciences, vol. 60, pp. 25–28.MathSciNetCrossRefGoogle Scholar
  35. MARSAGLIA, G. and ZAMAN, A. (1991): A new class of random number generators. Annals of Applied Probability, vol. 1, pp. 462–480.MathSciNetzbMATHCrossRefGoogle Scholar
  36. METROPOLIS, N., ROSENBLUTH, A., ROSENBLUTH, M., TELLER, A., and TELLER, E. (1953): Equations of state calculations by fast computing machines. Journal of Chemical Physics, vol. 21, p. 1087–1091.CrossRefGoogle Scholar
  37. MURDOCH, D.J. and GREEN, P.J. (1998): Exact sampling from a continous space. Scandinavian Journal of Statistics, vol. 25, pp. 483–502.MathSciNetzbMATHCrossRefGoogle Scholar
  38. PROPP, G.J. and WILSON, D.B. (1996): Exact sampling with coupled Markov chains and applications to statistical mechanics. Random Structures and Algorithms, vol. 9, pp. 223–252.MathSciNetzbMATH3.0.CO%3B2-O'>CrossRefGoogle Scholar
  39. RÖSLER, U. and RÜSHENDORF, L. (2001): The contraction method for recursive algorithms. Algorithmica, vol. 29, pp. 3–33.MathSciNetzbMATHCrossRefGoogle Scholar
  40. K. SATO (2000): Lévy Processes and Infinitely Divisible Distributions, Cambridge University Press, Cambridge.Google Scholar
  41. ULRICH, U. (1984): Computer generation of distributions on the m-sphere. Applied Statistics, vol. 33, pp. 158–163.MathSciNetzbMATHCrossRefGoogle Scholar
  42. VERVAAT, W. (1979): On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Advances in Applied Probability, vol. 11, pp. 750–783.MathSciNetzbMATHCrossRefGoogle Scholar
  43. VON NEUMANN, J. (1963): Various techniques used in connection with random digits. Collected Works, vol. 5, pp. 768–770, Pergamon Press. Also in (1951): Monte Carlo Method. National Bureau of Standards Series, Vol. 12, pp. 36-38.Google Scholar
  44. WILSON, D.B. (2000): Layered multishift coupling for use in perfect sampling algorithms (with a primer on CFTP). In: Monte Carlo Methods, Madras, N. (ed.), pp. 141–176, Fields Institute Communications, vol. 6, American Mathematical Society.Google Scholar
  45. ZOLOTAREV, V. M. (1959): On analytic properties of stable distribution laws. Selected Translations in Mathematical Statistics and Probability, vol. 1, pp. 207–211.Google Scholar
  46. ZOLOTAREV, V. M. (1966): On the representation of stable laws by integrals. Selected Translations in Mathematical Statistics and Probability, vol. 6, pp. 84–88.Google Scholar
  47. ZOLOTAREV, V. M. (1981): Integral transformations of distributions and estimates of parameters of multidimensional spherically symmetric stable laws. In: Contributions to Probability, pp. 283–305, Academic Press.Google Scholar
  48. ZOLOTAREV, V. M. (1986): One-Dimensional Stable Distributions, American Mathematical Society, Providence, R.I..Google Scholar